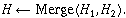Datastructures Important Questions

MODULE 1

Identify appropriate data structures for each of the following applications &
justify your selection.
i. Syntax Parsing- BST
ii. Priority Queue- Heap
iii. Symbol Table of compiler

Write and analyze the BST_Insert pseudocode.

We can sort a given set of n numbers by first building a binary search
tree containing these numbers (using TREE-INSERT repeatedly to insert the numbers one by one) and then printing the numbers by an inorder tree walk. What are the worst-case and best-case running times for this sorting algorithm?

Give a linear time algorithm for building heap and illustrate the same on the
array A :[5; 3; 17 ; l0; 84; 19; 6; 22; 9].

Algorithm for Building a heap:

A strict analysis of an algorithm generated the time complexity as a function f(n) : n3 + 3n2 * 3. Denote the complexity of the algorithm in Theta notation and justify your answer.

Write an algorithm to check whether a given binary tree is an AVL search tree

What is the advantage of heap over array in building a priority queue? Write an
algorithm to build a min-heap.

1.a Define abstract data type?

2. Give a method to find an element in a binary search tree?What is its advantage in terms of computational complexity?

3. List any 3 asymptotic notations with proper definitions?

4. Compare Binary Search Tree property and Heap property.Give a recursive procedure of the BST-INSERT procedure.

5. Explain The basic operations defined on a symbol table?

6. Illustrate the pseudo code for TREE-DELETE(T,z) for deleting a node z from BST T ?

Give the importance of asymptotic notation during analysis of algorithms. explain any 3 asymptotic notations with proper definitions.

A 3-ary max heap is like a binary max heap, but instead of 2 children, nodes have 3 children. A 3-ary heap can be represented by an array as follows: The root is stored in the first location, a[0], nodes in the next level, from left to right, is stored from a[1] to a[3]. The nodes from the second level of the tree from left to right are stored from a[4] location onward. An item x can be inserted into a 3-ary heap containing n items by placing x in the location a[n] and pushing it up the tree to satisfy the heap property. Check whether the sequence 9,6,3,1,8,5 is valid.

NOT Valid.

The sequence can be 9, 5, 6, 8, 3, 1

Compare BST property & Heap property. Give a recursive procedure of the BST-Insert procedure.

You need to find kth smallest element in a array. Suggest a method with best time complexity to solve this problem.

Create a max heap of size k from first k elements of array.
Scan all elements in array one by one. If current element is less than max on heap, add current element to heap and heapify. ...
At the end, max heap will contain k smallest elements of array and root will be kth smallest element.

Write a Recursive algorithm to check whether the tree is height balanced binary search tree

https://www.techiedelight.com/check-given-binary-tree-is-height-balanced-not/

Algorithm to build a heap on O(n) time. Prove its correctness.

MODULE 2

What is the advantage of a B* tree over a B tree in database indexing

Create an AVL tree for the sequence 21,44,12,56,5,49,63,24,96,34,3,42'
Write functions for AVL tree rotations

Derive the worst case search time of a redblack tree. What is the advantage of a
redblack tree over a binary search tree?

"Height of the B Tree grows only logarithmically wit the number of nodes it contains", Justify.

Draw complete binary search trees of height 3 with arbitrary 15 keys.
Add the NIL leaves and color the nodes in three different ways such that
the black-heights of the resulting red-black tree are 2,3 and4.

Insert 14, 17,11,7,53,4, 13 into an empty AVL tree

Consider the following splay tree: Perform a delete for key 3.

"Splay trees are self adjusting". Comment on the statement and briefly explain the splaying action of splay tree.

Create an AVL Tree from given set of values. H,I,J,B,A,E,C,F,D

Explain the linear linked list representation of Binary Tree.Mention the advantages and disadvantages of sequential representation

Choice of order is a decinding factor when we select B+ tree for database indexing. Justify?

Create a RBT for the sequence 29,44,12,53,5,49,63,24,96,33,2,45.

Derive the worst case search time of an AVL tree. What is the advantage of an AVL tree over a binary search tree?

MODULE 3

Write the algorithm for insertion in a skiplist

Create an treap for the sequence 28 , 46 ,32 , 53 ,23, gg ,32 ,5 , 41, 63 ,21, 96,
33, 2, 43,75, and 6l with node priorities same as that of key values.

What is the difference between amortized analysis and average case analysis?
Perform amortized analysis using aggregate and potential method on insert
operation of dynamic tables.

Discuss about Universal Hash Functions with example.

Let S be a stack data structure. It supports the following operations:

---Init(S): Create an empty ordered stack.
---Multi Push(S,x): Insert'x'two times to the stack.
---Multi_Pop(S,k): removes the k top objects of stack S, popping the
entire stack if the stack contalns fewer than k objects.

Do an amortized analysis using 'Potential Method' of the above operations.

Write the algorithms to perform insertion, deletion, and searching in skip lists
with proper examples.

Define the Trep data structure and its properties.Implement the treap using following elements (a,3), (b,9), (c,2), (e,6), (f,5). [Note: 9 has the highest priority and 2 has lowest priority]

explain extendable hashing in detail with an example? why we are going for dynamic hashing instead of static hashing. what are the advantages of dynamic hashing over static hashing. explain the disadvantages of dynamic hashing.

Explain the different methods of amortized analysis in detail in terms of stack operations.

Explain why a treap is considered as a randomized data structure

What is the difference between amortized analysis and average case analysis? Perform amortized analysis on insert operation of dynamic tables.

Develop algorithms to perform insertion, deletion, and search on a skiplist.

MODULE 4

1. What is the advantage of a skew heap over a leftist heap?

Skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree. Leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x.

Skew heaps are advantageous because of their ability to merge more quickly. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic.

2. Create a leftist heap using the sequence 34, 41, 5,25, 94,2, 55, 6,30, 9,20, 85,
and 49. Perform extract min once and show the resulting heap.

3. Consider a queuing system in which the elements are queued up according to 6
their priority. The system supports operation which will either remove elements
with highest priority or elements with least priority. Select a suitable data
structure for this system and develop algorithms for the same.

4. Discuss the advantages of leftist and skew heaps compared to binary heap.

Skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree.

Leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x.

Leftist trees are advantageous because of their ability to merge quickly, compared to binary heaps which take Θ(n).

In almost all cases, the merging of skew heaps has better performance. However merging leftist heaps has worst-case O(log n) complexity while merging skew heaps has only amortized O(log n) complexity.

5. Differentiate Height-biased and Weigbt-biased leftist trees.

Weight-Biased Leftist Trees in Data Structure

Here we will consider the number of nodes in a subtree, rather than the length of a shortest path for root to external node. Here we will define the weight w(x) of node x, to be the number of internal nodes in the subtree with root x. If x is an external node, then the weight is 0. If x is internal node, then the weight is one more than the sum of weights of its children.

Here is an example of Weight Biased Leftist Tree (WBLT) −

Suppose the Binary tree is like this −

If we calculate w(x) values for each node, it will be like this −

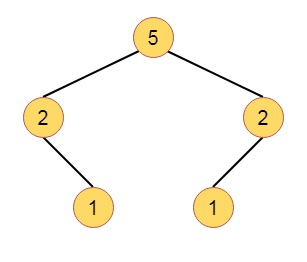
Now the definition of WBLT is like −

A binary tree is called Weight Balanced Leftist Tree if and only if, at every internal node the w(x) of left child is greater than or equal to the w(x) of the right child. A max (min) WBLT is a max (min) tree that is also a WBLT.

Height-Biased Leftist Trees in Data Structure

Consider a binary tree where a special node, called an external node replaces each empty subtree. All other nodes are called Internal Nodes. When some external nodes are added with some binary tree, then that is called an extended binary tree.

If we do not consider the leaf edges of this tree, then that is the actual binary tree. and this is the extended binary tree.

Now suppose s(x) be the length of a shortest path from node x to an external node in its subtree. If x is an external node, its s(x) value is 0. If the x is an internal node, the value is −

min{𝑠(𝐿), 𝑠(𝑅)} + 1

Here L and R are the left and right children of x. Now let us see the s values of the given tree.

The definition of the HBLT is like: A binary tree is a Height Balanced Leftist Tree (HBLT), if and only if, at every internal node, the s value of the left child is greater or equal to the s value of right child.

The above tree is not HBLT. The parent of node a, has s(L) = 0, and s(R) is 1, except that all other nodes are satisfying the rule of the HBLT. So if we left and right subtree of that node, to make it HBLT.

Some other definitions are −

A max tree (min tree) is a tree, in which the value of each node is greater (less) or equal to its children.
A max HBLT is an HBLT, that is also a max tree, a min HBLT is an HBLT, that is also a min tree.

6. Consider the array A: [3, 5, 6, 7, 20, 8, 2, 9, 12, 1 5,. 30, I 7]. Draw the
max leftist tree created from this aray.

7. How do we find the minimum and maximum elements in a min-max heap?

8. Consider the below min-max heap and perform delete Min and, delete Max from that.

9. what are the minimum and maximum number of elemnts a heap of height h? Show that an n-element has height logn(floor(logn)).

By the definition of a heap, all the tree levels are completely filled except possibly for the lowest level, which is filled from the left up to a point. Clearly a heap of height h has the minimum number of elements when it has just one node at the lowest level. The levels above the lowest level form a complete binary tree of height h -1 and 2^h-1 nodes. Hence the minimum number of nodes possible in a heap of height h is 2^h. Clearly a heap of height h, has the maximum number of elements when its lowest level is completely filled. In this case the heap is a complete binary tree of height h and hence has 2^h+1-1 nodes.

The number of edges on a simple downward path from a root to a leaf. Note that the height of a tree with n node is lg n which is (lgn). This implies that an n-element heap has height lg n

In order to show this let the height of the n-element heap be h. From the bounds obtained on maximum and minimum number of elements in a heap, we get

2^h ≤ n ≤ 2^h+1-1

Where n is the number of elements in a heap.

2^h ≤ n ≤ 2^h+1

Taking logarithms to the base 2

h ≤ lgn ≤ h +1

It follows that h = lgn.

10. Define Priority Queue and its properties. Mention the basic operations and its working of Priority Queue. Give the steps to implement stack using Priority Queue?

Priority Queue is an extension of queue with following properties.

Every item has a priority associated with it.
An element with high priority is dequeued before an element with low priority.
If two elements have the same priority, they are served according to their order in the queue.

A typical priority queue supports following operations.
insert(item, priority): Inserts an item with given priority.
getHighestPriority(): Returns the highest priority item.
deleteHighestPriority(): Removes the highest priority item.

Applications of Priority Queue:
1) CPU Scheduling
2) Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc
3) All queue applications where priority is involved.

A priority queue is implemented using Heap.

Algorithm

Create a class stack with the priority queue. In addition to queue initialise a variable count = 0 inside it.
Create function push() which accepts an integer value as a parameter. Increment the count and push the pair of count and element in the priority queue.
Create function top() and return the element stored in top i.e. second part of the pair stored at top of the priority queue.
After that, create function isEmpty(). Return true if the priority queue is empty else return false.
Similarly, create function pop() and check if queue is empty print “Empty Stack”. Else decrement the count and pop the top of the priority queue.
Finally, traverse the stack and while stack is not empty print the top and pop the top.

11. Steps for Merging Leftist Heaps

Compare the roots of two heaps.
Push the smaller key into an empty stack, and move to the right child of smaller key.
Recursively compare two keys and go on pushing the smaller key onto the stack and move to its right child.
Repeat until a null node is reached.
Take the last node processed and make it the right child of the node at top of the stack, and convert it to leftist heap if the properties of leftist heap are violated.
Recursively go on popping the elements from the stack and making them the right child of new stack top.

12. Explain any one applications of a mergeable heap

13. Define a skew heap a an abstract data type. Develop algorithms for ADT operations on a skew heap.

A Skew Heap is simply a binary tree. Values are stored in the structure, one per node, satisfying the heap-order property: A value stored at a node is larger than the value stored at its parent, except for the root (as root has no parent).

Operations:

1. Merging two heaps

When two skew heaps are to be merged, we can use a similar process as the merge of two leftist heaps:

Compare roots of two heaps; let p be the heap with the smaller root, and q be the other heap. Let r be the name of the resulting new heap.
Let the root of r be the root of p (the smaller root), and let r's right subtree be p's left subtree.
Now, compute r's left subtree by recursively merging p's right subtree with q.

2. Adding values

Adding a value to a skew heap is like merging a tree with one node together with the original tree.

3. Removing values

Removing the first value in a heap can be accomplished by removing the root and merging its child subtrees.

*Consider a queuing system in which the elements are queued up according to their priority. the system supports operation which will either remove elements with highest priority or elements with least priority. Select a suitable data structure for this system and develop algorithms for the same.

MODULE 5

1. State and prove the properties of a binomial tree.

2. Conduct a complexity analysis of Dijkstra's algorithm using Fibonacci heap and justify its advantage over an array and a binary heap.

3. Construct a binomial heap using the sequence 35,56,23, 94, 13,2, 98,45,66, 20,93, and 67. Perform extract min once and show the resulting heap.

*How Fibonacci heap differ from Binomial Heap.

Describe the data structure Binomial Heap and the operation UNION using the
given heaps:

*Compare the differences while using a Fibonacci heap and a binary heap for
implementing dijisktra's algorithm. Which data structure provides better
implemention? Why?

*For the binomial tree Bk, Prove the following properties,

a. there are 2^k nodes

b. the height of the tree is k

*What are the differences between a Fibonacci heap and a binomial heap? Mention the differences in terms of implementation and complexity.

Write an re-implementation of Dijkstras algorithm for single source shortest using Fibonacci heap. Analyze your algorithm?

What is the advantage of a Fibonacci heap over a binomial heap?

Compare differences while using a Fibonacci heap and binary heap for implementation dijikstras algorithm. which data structure provides better implementation. Why?

*State and prove the properties of binomial trees.

MODULE 6

Why we need a multidimensional data structure?

Good storage utilization should be guaranteed (70% is sufficient)\
Simple tasks should require only a small number of disk accesses
Different dimensions should be treated in a symmetric way
„ Clustering of objects should conform with geometric proximity, to support efficient processing of range queries.
„The structure should enable dynamic reorganization, when the data set grows and shrinks (such as B-tree, linear hashing, etc.).
Algorithms for search and update should be simple.
„The structure should support different kinds of queries.

*Develop algorithms for insertion, find minimum and delete nodes from a K-D
tree. Insert into a 2-D tree the following elements in sequence (33,41), (25,27,),
(10,12), (55,70), (36,42), (39,22), 28,6l) , (21, l4), (31,39), (21,55).

Develop algorithm for insertion in an R tree.

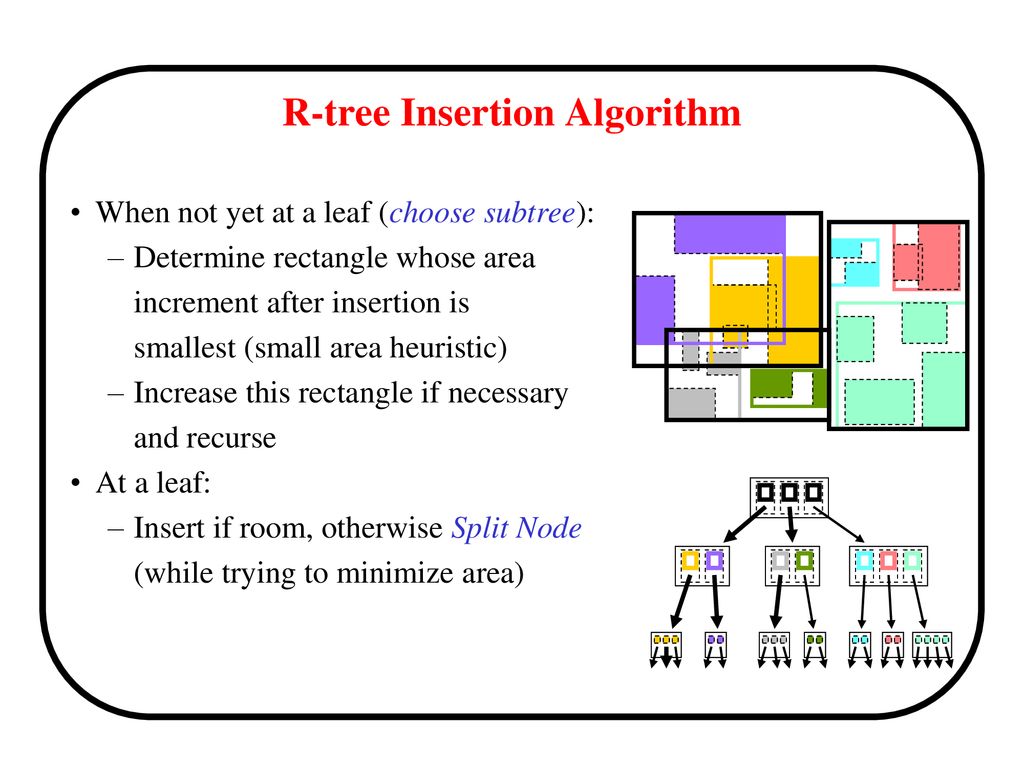
Identify and describe the data structure which is suitable for range queries with
multi-dimensional feature space.

Compare and contrast R-Tress with B-Trees. Discuss applications of R-trees.

Insert into a 2-D tree the following elements in sequence (39,46), (15,27),
(10,12), (75,7A), (30,43), (38,22), (48,6) , (2r, t4), (3,39), 2l,5). How it
differs from quad trees.

Give the applications of Quad trees

Quadtrees are trees used to efficiently store data of points on a two-dimensional space. In this tree, each node has at most four children.

*Develop algorithms for insertion, find minimum and delete nodes from a K-D tree. Insert into a2D tree the following elements in sequence (30,40), (5,25),(10,12),(70,70), (50,30),(35,45), (45,66), (2,44), ((43,69),(22,35).

*Compare MX Quad tree and KD tree? Write the applications of KD Tree, MX Quad Tree and R Tree.

k-d trees are a useful data structure for several applications, such as searches involving a multidimensional search key (e.g. range searches and nearest neighbor searches) and creating point clouds. k-d trees are a special case of binary space partitioning trees.

Quadtrees are trees used to efficiently store data of points on a two-dimensional space. In this tree, each node has at most four children.

R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons.

Suggest any application in which a multidimensional search structure is necessary.

*Develop algorithms for insertion, find minumum and delete nodes from a KD tree. Insert into a 2D tree the following elemnts in sequence (35,46), (15,29),(10,22), (78, 70), (30,40),(38,25),....

Explain how an MX Quad tree differ from a k-d tree? Explain the structure of an MX Quad tree with an example.

The difference (algorithmically) is: in quadtrees, the data reaching a node is split into a fixed (2^d), equal size cells, whereas in kdtrees, the data is split into two regions based on some data analysis (e.g. the median of some coordinate). Quadtrees do not scale well to high dimensions, due to the exponential dependency in the dimension. The data structures also differ in their query time complexities.

Since you're interested in 2D points, either data structure may work for you. KD trees are very easy to query for ranges, and are generally preferred over quadtrees. I suggest you use them.

Min Max Heap | Leftist Heaps | Skewed Heaps (M4)

Min Max Heap

A min-max heap is a complete binary tree data structure which combines the usefulness of both a min-heap and a max-heap, that is, it provides constant time retrieval and logarithmic time removal of both the minimum and maximum elements in it. This makes the min-max heap a very useful data structure to implement a double-ended priority queue.

Like binary min-heaps and max-heaps, min-max heaps support logarithmic insertion and deletion and can be built in linear time.
Min-max heaps are often represented implicitly in an array; hence it's referred to as an implicit data structure.

The min-max heap property is: each node at an even level in the tree is less than all of its descendants, while each node at an odd level in the tree is greater than all of its descendants.

The structure can also be generalized to support other order-statistics operations efficiently, such as find-median, delete-median,find(k) (determine the kth smallest value in the structure) and the operation delete(k) (delete the kth smallest value in the structure), for any fixed value (or set of values) of k. These last two operations can be implemented in constant and logarithmic time, respectively.

The notion of min-max ordering can be extended to other structures based on the max- or min-ordering, such as leftist trees, generating a new (and more powerful) class of data structures.
A min-max heap can also be useful when implementing an external quick sort.

A min-max heap is a complete binary tree containing alternating min (or even) and max (or odd) levels. Even levels are for example 0, 2, 4, etc, and odd levels are respectively 1, 3, 5, etc. We assume in the next points that the root element is at the first level, i.e., 0.

Each node in a min-max heap has a data member (usually called key) whose value is used to determine the order of the node in the min-max heap.
The root element is the smallest element in the min-max heap.
One of the two elements in the second level, which is a max (or odd) level, is the greatest element in the min-max heap
Let $x$ be any node in a min-max heap.
- If $x$ is on a min (or even) level, then $x.key$ is the minimum key among all keys in the subtree with root $x$ .
- If $x$ is on a max (or odd) level, then $x.key$ is the maximum key among all keys in the subtree with root $x$ .
A node on a min (max) level is called a min (max) node.

A max-min heap is defined analogously; in such a heap, the maximum value is stored at the root, and the smallest value is stored at one of the root's children.

Mergeable Heaps

A "mergeable heap" is an ADT that stores an element from an ordered set, and supports the operations Insert, Min, and Extract-Min (just like priority queues). Mergeable heaps support an additional operation:

Merge() takes two mergeable heaps and returns one that contains all of the elements. Duplicates are preserved.

Two implementations of the mergeable heap are the "leftist tree" and the "binomial heap". We'll talk about leftist trees in this lecture.

A "leftist tree" is an implementation of a mergeable heap.

Leftist Heaps

Leftist heap is a priority queue implemented with a variant of a binary heap.
Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x.
In contrast to a binary heap, a leftist tree attempts to be very unbalanced.
In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.

The s-value (or rank) of a node is the distance from that node to the nearest leaf in the subtree rooted at that node.

A leftist tree is a binary tree with properties:

Normal Min Heap Property
Heavier on left side- the left subtree is usually taller than the right subtree.

From above second property, we can draw two conclusions :

The path from root to rightmost leaf is the shortest path from root to a leaf.
If the path to rightmost leaf has x nodes, then leftist heap has atleast 2^x – 1 nodes. This means the length of path to rightmost leaf is O(log n) for a leftist heap with n nodes.

A leftist tree is a mergeable heap. When inserting a new node into a tree, a new one-node tree is created and merged into the existing tree. To delete an item, it is replaced by the merge of its left and right sub-trees. Both these operations take O(log n) time. For insertions, this is slower than Fibonacci heaps, which support insertion in O(1) (constant) amortized time, and O(log n) worst-case.

Operations :

The main operation is merge().
deleteMin() (or extractMin() can be done by removing root and calling merge() for left and right subtrees.
insert() can be done be create a leftist tree with single key (key to be inserted) and calling merge() for given tree and tree with single node.

Leftist trees are advantageous because of their ability to merge quickly, compared to binary heaps which take Θ(n).

Skewed Heaps

A skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied:

The general heap order must be enforced
Every operation (add, remove_min, merge) on two skew heaps must be done using a special skew heap merge.

Skew heaps may be described with the following recursive definition:

A heap with only one element is a skew heap.
The result of skew merging two skew heaps $sh_{1}$ and $sh_{2}$ is also a skew heap.

A skew heap is a self-adjusting form of a leftist heap which attempts to maintain balance by unconditionally swapping all nodes in the merge path when merging two heaps. (The merge operation is also used when adding and removing values.) With no structural constraints, it may seem that a skew heap would be horribly inefficient.

However, amortized complexity analysis can be used to demonstrate that all operations on a skew heap can be done in O(log n). In fact, with ${\textstyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ denoting the golden ratio, the exact amortized complexity is known to be log_φ n (approximately 1.44 log₂ n).

Operations:

1. Merging two heaps

When two skew heaps are to be merged, we can use a similar process as the merge of two leftist heaps:

Compare roots of two heaps; let p be the heap with the smaller root, and q be the other heap. Let r be the name of the resulting new heap.
Let the root of r be the root of p (the smaller root), and let r's right subtree be p's left subtree.
Now, compute r's left subtree by recursively merging p's right subtree with q.