Evolutionary computation is an area of computer science that uses ideas from biological evolution to solve computational problems.
There are several approaches that have been followed in the field of evolutionary computation. The general term for such approaches is evolutionary algorithms.
Genetic Algorithms (GA),
Evolutionary Strategies (ES)
Evolutionary Programming (EP)
Genetic Programming (GP)
Among this, The most widely used form of evolutionary algorithms are genetic algorithms (GAs),
Genetic algorithms (GAs), mainly operates on binary strings and uses a recombination operator with mutation as a background operator.
Evolution strategies (ESs) were developed as a method to solve parameter optimization problems.
Evolutionary programming (EP) techniques aimed at evolution of artificial intelligence, and finite state machines (FSM) were selected as a chromosomal representation of individuals.
Genetic programming (GP) techniques provide a way to run a search of the space of possible computer programs for the best one.
#Representing the different types of EAs
Historically different flavors of EAs have been associated with different representations,
Binary strings : Genetic Algorithms
Real-valued vectors : Evolution Strategies
Finite state Machines: Evolutionary Programming
LISP trees: Genetic Programming

Multiple business benefits are associated with evolutionary algorithms, including:
- Increased flexibility. Evolutionary algorithm concepts can be modified and adapted to solve the most complex problems humans face and meet target objectives.
- Better optimization. The vast “population” of all possible solutions is taken into consideration. This means the algorithm is not restricted to a particular solution.
- Unlimited solutions. Unlike classical
methods that present and attempt to maintain a single best solution,
evolutionary algorithms include and can present multiple potential
solutions to a problem.
Genetic Algorithms (GA)
- Genetic Algorithms (GAs) are search based algorithms based on the concepts of natural selection and genetics.
- Genetic algorithms are a type of optimization algorithm, meaning they are used to find the optimal solution(s) to a given computational problem that maximizes or minimizes a particular function.
- Genetic algorithms represent one branch of the field of study called evolutionary computation, in that they imitate the biological processes of reproduction and natural selection to solve for the ‘fittest’ solution.
The simplest version of a genetic algorithm consists of the following components:
#Population (Set Of Chromosomes)
It is a subset of all the possible (encoded) solutions to the given problem.
- Chromosomes − A chromosome is one such solution to the given problem.
Gene − A gene is one element position of a chromosome.
Allele − It is the value a gene takes for a particular chromosome.
#Fitness function
Assigns a numerical value to each chromosome in the population measuring its quality as a candidate solution to the problem at hand.
#Genetic operators
- Operators to be applied to the chromosomes to create a new population.
- These typically include selection, in which the fittest chromosomes are chosen to produce offspring;
- crossover, in which two parent chromosomes recombine their genes to produce one or more offspring chromosomes; and
- mutation, in which one or more genes in an offspring are modified in some random fashion.
A typical GA carries out the following steps:
- Initialize the population of n chromosomes randomly.
- Calculate the fitness f (x) of each chromosome x in the population.
- Repeat the following steps until n offspring have been created:
- Select a pair of parent chromosomes from the current population.
- Perform Crossover & Mutation (typically replaces the current value of a locus (eg: 0) with another value (eg: 1)).
- Replace the current population with the new population.
- Repeat steps from 2 until the criteria is achieved.
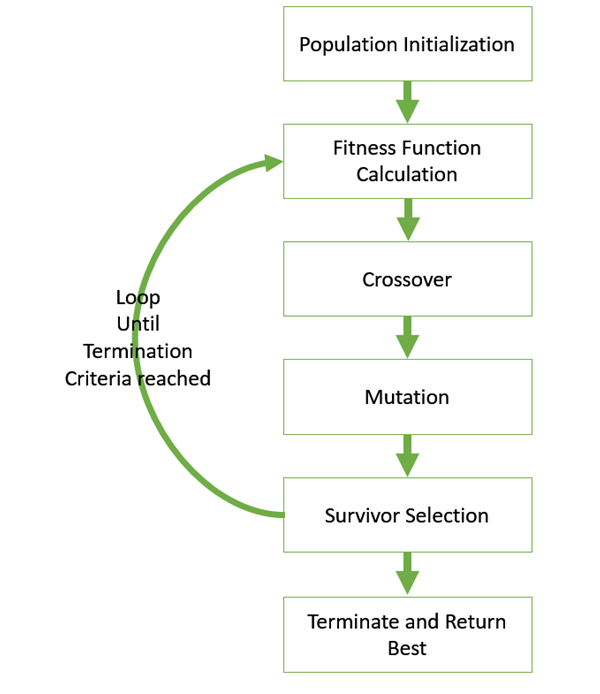
Each iteration of this process is called a generation.
Evolutionary Strategies (ES)
- An evolution strategy (ES) is an optimization technique based on ideas of evolution.
- The 'evolution strategy' optimization technique was created in the early 1960s and developed further in the 1970s and later by Ingo Rechenberg, Hans-Paul Schwefel and their co-workers.
- Evolution strategies use natural problem-dependent representations, and primarily mutation and selection, as search operators.
- In common with evolutionary algorithms, the operators are applied in a loop.
- An iteration of the loop is called a generation. The sequence of generations is continued until a termination criterion is met.
Evolutionary Programming (EP)
- Evolutionary programming is one of the four major evolutionary algorithm paradigms.
- It is similar to genetic programming, but the structure of the program to be optimized is fixed, while its numerical parameters are allowed to evolve.
- It was first used by Lawrence J. Fogel in the US in 1960 in order to use simulated evolution as a learning process aiming to generate artificial intelligence.
- Fogel used finite-state machines as predictors and evolved them. Currently evolutionary programming is a wide evolutionary computing dialect with no fixed structure or (representation), in contrast with some of the other dialects. It is becoming harder to distinguish from evolutionary strategies.
- Its main variation operator is mutation; members of the population are viewed as part of a specific species rather than members of the same species therefore each parent generates an offspring, using a survivor selection.
Genetic Programming (GP)
- Genetic programming is indeed a special type of genetic algorithm. The difference lies in their representations. Genetic programming adopts trees as genotypes to represent programs or expressions.
- The typical selection schemes of evolutionary algorithms can still be used as parent selection and survival selection in genetic programming.
- The distinct features of genetic programming are their crossover and mutation operators.
- For instance, swapping sub-trees between two trees and random generation of sub-trees.
GP can be used to discover a functional relationship between features in data (symbolic regression), to group data into categories (classification), and to assist in the design of electrical circuits, antennae, and quantum algorithms. GP is applied to software engineering through code synthesis, genetic improvement, automatic bug-fixing, and in developing game-playing strategies, … and more.
Advantages of EA
- Evolutionary algorithm optimizers are global optimization methods and scale well to higher dimensional problems.
- They are robust with respect to noisy evaluation functions, and the handling of evaluation functions which do not yield a sensible result in given period of time is straightforward.
- The algorithms can easily be adjusted to the problem at hand.
- Almost
any aspect of the algorithm may be changed and customized.
- EA can be efficiently used for highly complex problems with multi-objectivity, non-linearity etc
- Provides not only a single best solution, but the 2 nd best, 3 rd best and so on as required.
- Gives quick approximate solutions.
- Can incorporate with other local search algorithms
Disadvantages
On the
other hand, although lots of research has been done on which
evolutionary algorithm is best suited for a given problem, this
question has not been answered satisfactorily. While the standard
values usually provide reasonably good performance, different
configurations may give better results. Furthermore, premature
convergence to a local extremum may result from adverse configuration
and not yield (a point near) the global extremum.
- Optimal solution cannot be ensured on using EA methods
- Convergence of EA techniques are problem oriented
- Sensitivity analysis should be carried out to find out the range in which the model is efficient
- Implementation requires good programming skill
Applications of EA
- Clustering, using genetic algorithms to optimize a wide range of different fit-functions.
- Multidimensional systems.
- Multimodal Optimization.
- Multiple criteria production scheduling.
- Multiple population topologies and interchange methodologies.
- Mutation testing