cs.lectures: Multi-Dimensional Structures

Multi-Dimensional Structures:
Segment Trees, K-D Trees, Point Quad Trees, MX-Quad Trees, R-
Trees, Applications of Multidimensional Structures.

Multidimensional structures or hypercubes are commonly used in OLAP to store and organize data to optimize query response time.

Segment Tree

Segment Tree is a basically a binary tree used for storing the intervals or segments.
Each node in the Segment Tree represents an interval.
Consider an array A of size N and a corresponding Segment Tree T

The root of $T$ T will represent the whole array $A [0 : N - 1]$ $A [0 : N - 1]$

Each leaf in the Segment Tree $T$ will represent a single element

The internal nodes in the Segment Tree $T$ represents the union of elementary intervals. $A [i : j]$ $0 \leq i < j < N$ $0 \leq i < j < N$

The root of the Segment Tree represents the whole array $A [0 : N - 1]$ .
Then it is broken down into two half intervals or segments and the two children of the root.
So in each step, the segment is divided into half and the two children represent those two halves.
So the height of the segment tree will be logn. $l o g_{2} N$ $l o g_{2} N$
There are N $N$ leaves representing the N $N$ elements of the array.
The number of internal nodes is N-1. $N - 1$ $N - 1$
So, a total number of nodes are 2(N-1) $2 \times N - 1$ $2 \times N - 1$

Once the Segment Tree is built, its structure cannot be changed. We can update the values of nodes but we cannot change its structure. Segment tree provides two operations:

Update: To update the element of the array and reflect the corresponding change in the Segment tree.

Query: In this operation we can query on an interval or segment and return the answer to the problem (say minimum/maximum/summation in the particular segment).

A Segment Tree can be built using recursion (bottom-up approach )

Representation of Segment trees
1. Leaf Nodes are the elements of the input array.
2. Each internal node represents some merging of the leaf nodes. The merging may be different for different problems. For this problem, merging is sum of leaves under a node.
An array representation of tree is used to represent Segment Trees. For each node at index i, the left child is at index 2*i+1, right child at 2*i+2 and the parent is at ⌊(i – 1) / 2⌋.

Time Complexity:
Time Complexity for tree construction is O(n). There are total 2n-1 nodes, and value of every node is calculated only once in tree construction.
Time complexity to query is O(Logn). To query a sum, we process at most four nodes at every level and number of levels is O(Logn).
The time complexity of update is also O(Logn). To update a leaf value, we process one node at every level and number of levels is O(Logn).

KD Tree

A K-D Tree(also called as K-Dimensional Tree) is a binary search tree where data in each node is a K-Dimensional point in space.
In short, it is a space partitioning(details below) data structure for organizing points in a K-Dimensional space.
A non-leaf node in K-D tree divides the space into two parts, called as half-spaces.
Points to the left of this space are represented by the left subtree of that node and points to the right of the space are represented by the right subtree.

How to determine if a point will lie in the left subtree or in right subtree?

If the root node is aligned in planeA, then the left subtree will contain all points whose coordinates in that plane are smaller than that of root node. Similarly, the right subtree will contain all points whose coordinates in that plane are greater-equal to that of root node.

Creation of a 2-D Tree:
Consider following points in a 2-D plane:
(3, 6), (17, 15), (13, 15), (6, 12), (9, 1), (2, 7), (10, 19)

Insert (3, 6): Since tree is empty, make it the root node.
Insert (17, 15): Compare it with root node point. Since root node is X-aligned, the X-coordinate value will be compared to determine if it lies in the rightsubtree or in the right subtree. This point will be Y-aligned.
Insert (13, 15): X-value of this point is greater than X-value of point in root node. So, this will lie in the right subtree of (3, 6). Again Compare Y-value of this point with the Y-value of point (17, 15) (Why?). Since, they are equal, this point will lie in the right subtree of (17, 15). This point will be X-aligned.
Insert (6, 12): X-value of this point is greater than X-value of point in root node. So, this will lie in the right subtree of (3, 6). Again Compare Y-value of this point with the Y-value of point (17, 15) (Why?). Since, 12 < 15, this point will lie in the left subtree of (17, 15). This point will be X-aligned.
Insert (9, 1):Similarly, this point will lie in the right of (6, 12).
Insert (2, 7):Similarly, this point will lie in the left of (3, 6).
Insert (10, 19): Similarly, this point will lie in the left of (13, 15).

ktree_1

Finding the element

For example, consider below KD Tree, if given dimension is x, then output should be 5 and if given dimensions is y, then output should be 12.

In KD tree, points are divided dimension by dimension. For example, root divides keys by dimension 0, level next to root divides by dimension 1, next level by dimension 2 if k is more then 2 (else by dimension 0), and so on.

To find minimum we traverse nodes starting from root.
If dimension of current level is same as given dimension, then required minimum lies on left side if there is left child. This is same as Binary Search Tree Minimum.

Above is simple, what to do when current level’s dimension is different. When dimension of current level is different, minimum may be either in left subtree or right subtree or current node may also be minimum. So we take minimum of three and return. This is different from Binary Search tree.

Deletion

1. If current node contains the point to be deleted

If node to be deleted is a leaf node, simply delete it (Same as BST Delete)
If node to be deleted has right child as not NULL (Different from BST)
1. Find minimum of current node’s dimension in right subtree.
2. Replace the node with above found minimum and recursively delete minimum in right subtree.
Else If node to be deleted has left child as not NULL (Different from BST)
1. Find minimum of current node’s dimension in left subtree.
2. Replace the node with above found minimum and recursively delete minimum in left subtree.
3. Make new left subtree as right child of current node.

2. If current doesn’t contain the point to be deleted

If node to be deleted is smaller than current node on current dimension, recur for left subtree.
Else recur for right subtree.

Example of Delete:
Delete (30, 40): Since right child is not NULL and dimension of node is x, we find the node with minimum x value in right child. The node is (35, 45), we replace (30, 40) with (35, 45) and delete (30, 40).

Delete (70, 70): Dimension of node is y. Since right child is NULL, we find the node with minimum y value in left child. The node is (50, 30), we replace (70, 70) with (50, 30) and recursively delete (50, 30) in left subtree. Finally we make the modified left subtree as right subtree of (50, 30).

Point quadtree

A quadtree is a tree data structure in which each internal node has exactly four children. Quadtrees are the two-dimensional analog of octrees and are most often used to partition a two-dimensional space by recursively subdividing it into four quadrants or regions. The data associated with a leaf cell varies by application, but the leaf cell represents a "unit of interesting spatial information". The subdivided regions may be square or rectangular, or may have arbitrary shapes.

The point quadtree is an adaptation of a binary tree used to represent two-dimensional point data.
It shares the features of all quadtrees but is a true tree as the center of a subdivision is always on a point.
It is often very efficient in comparing two-dimensional, ordered data points, usually operating in O(log n) time.
Point quadtrees are worth mentioning for completeness, but they have been surpassed by k-d trees as tools for generalized binary search.

Point quadtrees are constructed as follows.

Given the next point to insert, we find the cell in which it lies and add it to the tree. The new point is added such that the cell that contains it is divided into quadrants by the vertical and horizontal lines that run through the point. Consequently, cells are rectangular but not necessarily square. In these trees, each node contains one of the input points.

Since the division of the plane is decided by the order of point-insertion, the tree's height is sensitive to and dependent on insertion order. Inserting in a "bad" order can lead to a tree of height linear in the number of input points (at which point it becomes a linked-list). If the point-set is static, pre-processing can be done to create a tree of balanced height.

Node structure for a point quadtree

A node of a point quadtree is similar to a node of a binary tree, with the major difference being that it has four pointers (one for each quadrant) instead of two ("left" and "right") as in an ordinary binary tree. Also a key is usually decomposed into two parts, referring to x and y coordinates. Therefore, a node contains the following information:

four pointers: quad[‘NW’], quad[‘NE’], quad[‘SW’], and quad[‘SE’]
point; which in turn contains:
- key; usually expressed as x, y coordinates
- value; for example a name
R Tree
- R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons.
A common real-world usage for an R-tree might be to store spatial objects such as restaurant locations or the polygons that typical maps are made of: streets, buildings, outlines of lakes, coastlines, etc. and then find answers quickly to queries such as "Find all museums within 2 km of my current location", "retrieve all road segments within 2 km of my location" (to display them in a navigation system) or "find the nearest gas station" (although not taking roads into account). The R-tree can also accelerate nearest neighbor search^[4] for various distance metrics, including great-circle distance.^[5]
R-trees are highly useful for spatial data queries and storage. Some of the real life applications are mentioned below:
- Indexing multi-dimensional information.
- Handling geospatial coordinates.
- Implementation of virtual maps.
- Handling game data.
Properties of R-tree:
Consists of a single root, internals nodes and leaf nodes.
Root contains the pointer to the largest region in the spatial domain.
Parent nodes contains pointers to their child nodes where region of child nodes completely overlaps the regions of parent nodes.
Leaf nodes contains data about the MBR to the current objects.
MBR-Minimum bounding region refers to the minimal bounding box parameter surrounding the region/object under consideration.

Example: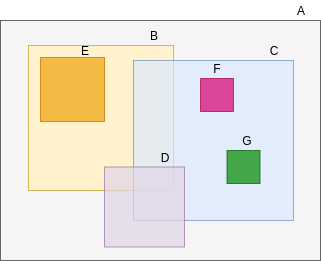
R-Tree
R-Tree Represesntation: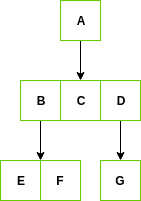
Tree representation

Comparison with Quad-trees:

Tiling level optimization is required in Quad-trees whereas in R-tree doesn’t require any such optimization.
Quad-tree can be implemented on top of existing B-tree whereas R-tree follow a different structure from a B-tree.
Spatal index creation in Quad-trees is faster as compared to R-trees.
R-trees are faster than Quad-trees for Nearest Neighbour queries while for window queries, Quad-trees are faster than R-trees.

cs.lectures

Multi-Dimensional Structures

Point quadtree

Node structure for a point quadtree

No comments:

Post a Comment

Monk and Inversions