Min Max Heap

A min-max heap is a complete binary tree data structure which combines the usefulness of both a min-heap and a max-heap, that is, it provides constant time retrieval and logarithmic time removal of both the minimum and maximum elements in it. This makes the min-max heap a very useful data structure to implement a double-ended priority queue.

Like binary min-heaps and max-heaps, min-max heaps support logarithmic insertion and deletion and can be built in linear time.
Min-max heaps are often represented implicitly in an array; hence it's referred to as an implicit data structure.

The min-max heap property is: each node at an even level in the tree is less than all of its descendants, while each node at an odd level in the tree is greater than all of its descendants.

The structure can also be generalized to support other order-statistics operations efficiently, such as find-median, delete-median,find(k) (determine the kth smallest value in the structure) and the operation delete(k) (delete the kth smallest value in the structure), for any fixed value (or set of values) of k. These last two operations can be implemented in constant and logarithmic time, respectively.

The notion of min-max ordering can be extended to other structures based on the max- or min-ordering, such as leftist trees, generating a new (and more powerful) class of data structures.
A min-max heap can also be useful when implementing an external quick sort.

A min-max heap is a complete binary tree containing alternating min (or even) and max (or odd) levels. Even levels are for example 0, 2, 4, etc, and odd levels are respectively 1, 3, 5, etc. We assume in the next points that the root element is at the first level, i.e., 0.

Each node in a min-max heap has a data member (usually called key) whose value is used to determine the order of the node in the min-max heap.
The root element is the smallest element in the min-max heap.
One of the two elements in the second level, which is a max (or odd) level, is the greatest element in the min-max heap
Let $x$ be any node in a min-max heap.
- If $x$ is on a min (or even) level, then $x.key$ is the minimum key among all keys in the subtree with root $x$ .
- If $x$ is on a max (or odd) level, then $x.key$ is the maximum key among all keys in the subtree with root $x$ .
A node on a min (max) level is called a min (max) node.

A max-min heap is defined analogously; in such a heap, the maximum value is stored at the root, and the smallest value is stored at one of the root's children.

Mergeable Heaps

A "mergeable heap" is an ADT that stores an element from an ordered set, and supports the operations Insert, Min, and Extract-Min (just like priority queues). Mergeable heaps support an additional operation:

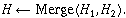
Merge() takes two mergeable heaps and returns one that contains all of the elements. Duplicates are preserved.

Two implementations of the mergeable heap are the "leftist tree" and the "binomial heap". We'll talk about leftist trees in this lecture.

A "leftist tree" is an implementation of a mergeable heap.

Leftist Heaps

Leftist heap is a priority queue implemented with a variant of a binary heap.
Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x.
In contrast to a binary heap, a leftist tree attempts to be very unbalanced.
In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.

The s-value (or rank) of a node is the distance from that node to the nearest leaf in the subtree rooted at that node.

A leftist tree is a binary tree with properties:

Normal Min Heap Property
Heavier on left side- the left subtree is usually taller than the right subtree.

From above second property, we can draw two conclusions :

The path from root to rightmost leaf is the shortest path from root to a leaf.
If the path to rightmost leaf has x nodes, then leftist heap has atleast 2^x – 1 nodes. This means the length of path to rightmost leaf is O(log n) for a leftist heap with n nodes.

A leftist tree is a mergeable heap. When inserting a new node into a tree, a new one-node tree is created and merged into the existing tree. To delete an item, it is replaced by the merge of its left and right sub-trees. Both these operations take O(log n) time. For insertions, this is slower than Fibonacci heaps, which support insertion in O(1) (constant) amortized time, and O(log n) worst-case.

Operations :

The main operation is merge().
deleteMin() (or extractMin() can be done by removing root and calling merge() for left and right subtrees.
insert() can be done be create a leftist tree with single key (key to be inserted) and calling merge() for given tree and tree with single node.

Leftist trees are advantageous because of their ability to merge quickly, compared to binary heaps which take Θ(n).

In almost all cases, the merging of skew heaps has better performance. However merging leftist heaps has worst-case O(log n) complexity while merging skew heaps has only amortized O(log n) complexity.

Skewed Heaps

A skew heap (or self-adjusting heap) is a heap data structure implemented as a binary tree. Skew heaps are advantageous because of their ability to merge more quickly than binary heaps. In contrast with binary heaps, there are no structural constraints, so there is no guarantee that the height of the tree is logarithmic. Only two conditions must be satisfied:

The general heap order must be enforced
Every operation (add, remove_min, merge) on two skew heaps must be done using a special skew heap merge.

Skew heaps may be described with the following recursive definition:

A heap with only one element is a skew heap.
The result of skew merging two skew heaps $sh_{1}$ and $sh_{2}$ is also a skew heap.

A skew heap is a self-adjusting form of a leftist heap which attempts to maintain balance by unconditionally swapping all nodes in the merge path when merging two heaps. (The merge operation is also used when adding and removing values.) With no structural constraints, it may seem that a skew heap would be horribly inefficient.

However, amortized complexity analysis can be used to demonstrate that all operations on a skew heap can be done in O(log n). In fact, with ${\textstyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$ denoting the golden ratio, the exact amortized complexity is known to be log_φ n (approximately 1.44 log₂ n).

Operations:

1. Merging two heaps

When two skew heaps are to be merged, we can use a similar process as the merge of two leftist heaps:

Compare roots of two heaps; let p be the heap with the smaller root, and q be the other heap. Let r be the name of the resulting new heap.
Let the root of r be the root of p (the smaller root), and let r's right subtree be p's left subtree.
Now, compute r's left subtree by recursively merging p's right subtree with q.