A binary search tree is a organized data structure that quickly allows us to maintain a sorted list of numbers.
- It is called a binary tree because each tree node has a maximum of two children.
- It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time.
- The search tree data structure supports many dynamic-set operations, including SEARCH, MINIMUM, MAXIMUM , PREDECESSOR , SUCCESSOR , INSERT , and DELETE . Thus, we can use a search tree both as a dictionary and as a priority queue.
- In addition to a key and satellite data, each node contains attributes left, right, and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively.
- The keys in a binary search tree are always stored in such a way as to satisfy the
binary-search-tree property:
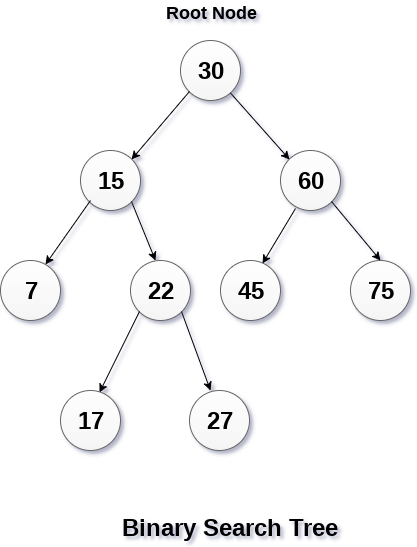
The properties that separate a binary search tree from a regular binary tree is.
- All nodes of the left sub-tree are less than the root node
- All nodes of the right sub-tree are more than the root node
- Both sub-trees of each node are also BST's i.e. they have the above two properties.
The binary-search-tree property allows us to print out all the keys in a binary
search tree in sorted order by a simple recursive algorithm, called an inorder tree
walk. (Similarly, a preorder tree walk prints the root before the values in either subtree,
and a postorder tree walk prints the root after the values in its subtrees.)
Advantages of using a BST
- Searching become very efficient in a binary search tree since, we get a hint at each step, about which sub-tree contains the desired element.
- The binary search tree is considered an efficient data structure in comparison to arrays and linked lists. In the searching process, it removes half sub-tree at every step. Searching for an element in a binary search tree takes o(log2n) time. In the worst case, the time it takes to search an element is 0(n).
- It also speeds up the insertion and deletion operations as compared to that in the array and linked list.

