Binary Search Tree (M1.3)

A binary search tree is a organized data structure that quickly allows us to maintain a sorted list of numbers.

• It is called a binary tree because each tree node has a maximum of two children.
• It is called a search tree because it can be used to search for the presence of a number in O(log(n)) time. 
•  The search tree data structure supports many dynamic-set operations, including SEARCH, MINIMUM, MAXIMUM , PREDECESSOR , SUCCESSOR , INSERT , and DELETE . Thus, we can use a search tree both as a dictionary and as a priority queue.
• In addition to a key and satellite data, each node contains attributes left, right, and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively.
• The keys in a binary search tree are always stored in such a way as to satisfy the
  binary-search-tree property: 
  

 

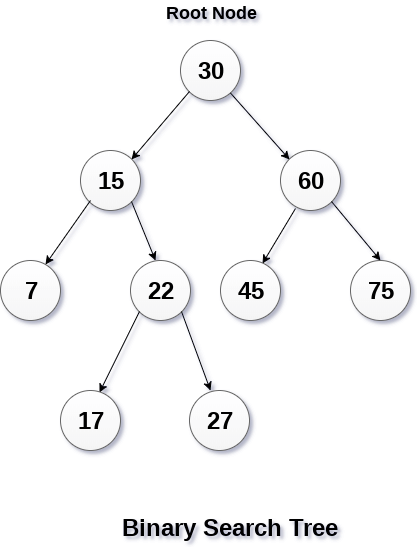
The properties that separate a binary search tree from a regular binary tree is.

 

1. All nodes of the left sub-tree are less than the root node
2. All nodes of the right sub-tree are more than the root node
3. Both sub-trees of each node are also BST's i.e. they have the above two properties.

The binary-search-tree property allows us to print out all the keys in a binary
search tree in sorted order by a simple recursive algorithm, called an inorder tree
walk. (Similarly, a preorder tree walk prints the root before the values in either subtree,
and a postorder tree walk prints the root after the values in its subtrees.)

 

 

Advantages of using a BST

 

1. Searching become very efficient in a binary search tree since, we get a hint at each step, about which sub-tree contains the desired element.
2. The binary search tree is considered an efficient data structure in comparison to arrays and linked lists. In the searching process, it removes half sub-tree at every step. Searching for an element in a binary search tree takes o(log2n) time. In the worst case, the time it takes to search an element is 0(n).
3. It also speeds up the insertion and deletion operations as compared to that in the array and linked list. 

 

 Disadvantages

 

1. The degree of the tree will always increase, resulting in low efficiency of search.

 

Quick Recap