Complexity- Analysis- Asymptotic Notations
The complexity of an algorithm is a function describing the efficiency of the algorithm in terms of the amount of data that the algorithm must process.
In simple, it is the measure of the amount of time or space required by an algorithm for an input of a given size (n).
There are two main complexity measures of the efficiency of an algorithm:
Time complexity
- It is nothing but the measure of the amount of time that is required by an algorithm for a given input of size (n).
- The “Time” can be the number of memory accesses performed or the number of comparisons between integers, the number of times some inner loop is executed, or some other natural unit related to the amount of real-time the algorithm will take.
Space complexity
- It is similar to the time complexity but here we consider the amount of memory (space) that an algorithm takes for the given input.
- Space complexity is sometimes ignored because the space used is minimal or obvious, but sometimes it becomes as important an issue as time.
What is the Analysis of Algorithms?
The analysis of the algorithm simply means to compare the various algorithms to solve the same problem. This is done to analyse which algorithm takes fewer resources like, time, effort and memory to solve a particular problem.
Types of analysis of an algorithm
To analyze a particular algorithm, first, we need to understand which input to the algorithm takes less time and for which input it takes more time. Based on this, we divide the inputs in three cases:
1. Best case where we assume the input, for which algorithm takes less time.
2. Worst case where we assume the input, for which algorithm takes a long time.
3. Average case where the input lies in between best and worst case.
Asymptotic Notation
The standard mathematical notations of representing the complexity of an algorithm. If we want to calculate the time without execution, we consider the no. of iterations, frequency so to represent in a proper way we make use of asymptotic notations.
Types of Asymptotic Notation
1. Big-O Notation (Ο) — describes the worst-case scenario.
2. Omega Notation (Ω) — describes the best-case scenario.
3. Theta Notation (θ) — This notation represents the average complexity of an algorithm.
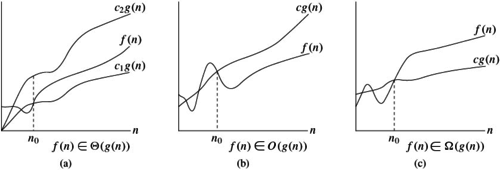
Big-O Notation (Ο)
- This notation is known as the asymptotic upper bound of the algorithm, or a Worst Case of an algorithm.
- It tells us that a certain function will never exceed a specified time for any value of the input n.
For a given function g(n), we denote by O(g(n)) the set of functions,
O(g(n)={f(n): there exist positive constants c and n0 such that 0 <= f(n) <= cg(n) for all n >= n0}
refer fig. b
Omega Notation (Ω)
- Big Omega notation is used to define the asymptotic lower bound of any algorithm or we can say the Best case of any algorithm.
- This always indicates the minimum time required for any algorithm for all input values, therefore the best case of any algorithm.
For a given function g(n), we denote by Ω(g(n)) the set of functions,
Ω(g(n)={f(n): there exist positive constants c and n0 such that 0 <= cg(n) <= f(n) for all n >= n0}
refer fig. c
Theta Notation (θ)
- Theta notation describes both upper bound and lower bound of an algorithm so we can say that it defines exact asymptotic behaviour.
- In the real case scenario the algorithm not always run on best and worst cases, the average running time lies between best and worst and can be represented by the theta notation.
For a given function g(n), we denote by θ(g(n)) the set of functions,
θ(g(n)={f(n): there exist positive constants c1, c2 and n0 such that 0 <= c1g(n) <= f(n) <= c2g(n) for all n >= n0}
refer fig. a
