B Tree & B+ Tree

B TREE

• It is a generalized form of the binary search tree / Extension of BST / Special type of BST
  
• It is also known as a height-balanced m-way search tree.
• B-tree is a special type of self-balancing search tree in which each node can contain more than one key and can have more than two children.  (i.e. if there is n children, there can be n-1 keys) 
  • NOTE: the no. of keys in a node & no. of children for a node depends on the order of B Tree. Every B Tree has a order m.
   
• Desined to work well on disks or other direct access secondary devices.
• Better at minimizing disk i/o operations. 

Why B-tree?

As we have said, B Tree is mainly used for disk access,So The need for B-tree arose with the rise in the need for accessing the physical storage media like a hard disk in less time. Even though, The secondary storage devices have larger capacity, they are slower in processing. There was a need for such types of data structures that minimize the disk accesses.

Other data structures such as a binary search tree, avl tree, red-black tree, etc can store only one key in one node. If you have to store a large number of keys, then the height of such trees becomes very large and the access time increases.

However, B-tree can store many keys in a single node and can have multiple child nodes. This decreases the height significantly allowing faster disk accesses.

One of the main reason of using B tree is its capability to store large number of keys in a single node and large key values by keeping the height of the tree relatively small.

B-tree Properties

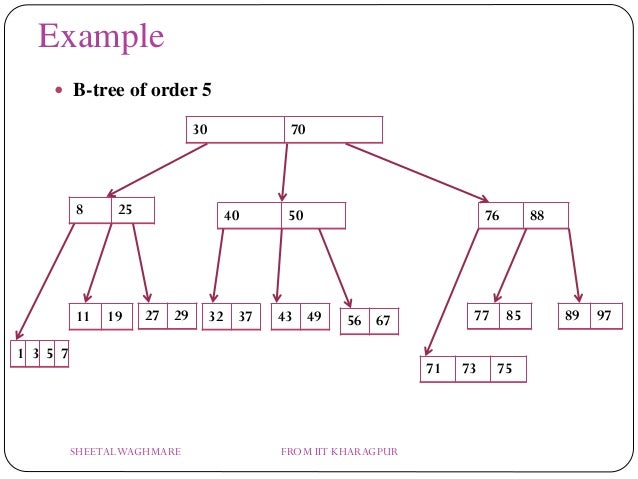
1. All leaf nodes must be at the same level. 

2. If n is the order of the tree, each internal node can contain at most n - 1 keys & have n no. of children.

3. Each node except root can have at most n children and at least n/2 children. 

4. The root has at least 2 children and contains a minimum of 1 key.

5. All nodes except root must have at least n/2 -1 keys & maximum of n-1 keys. 

6. All the key values in a node must be in Ascending Order.

For example, the following is an order-5 B-tree (m=5)

 

While performing some operations on B Tree, if any property of B Tree may get  violated (like min no. of nodes), so in that case we maintain the properties of B Tree, by borrowing from the immediate left or right node, or merging the nodes. 

Applications

Storing blocks of data: B tree is used to index the data and provides fast access to the actual data stored on the disks since, the access to value stored in a large database that is stored on a disk is a very time consuming process.

Multilevel Indexing: Searching an un-indexed and unsorted database containing n key values needs O(n) running time in worst case. However, if we use B Tree to index this database, it will be searched in O(log n) time in worst case.

 

Complexities

Worst case Time complexity: Θ(log n)

Average case Time complexity: Θ(log n)

Best case Time complexity: Θ(log n)

Average case Space complexity: Θ(n)

Worst case Space complexity: Θ(n)

 

B+ TREE 

 
B+ Tree is an extension of B Tree which allows efficient insertion, deletion and search operations. 

A B+ tree is an advanced form of a self-balancing tree in which all the values are present in the leaf level.

A B+ Tree is primarily utilized for implementing dynamic indexing on multiple levels. Compared to B- Tree, the B+ Tree stores the data pointers only at the leaf nodes of the Tree, which makes search more process more accurate and faster. 

The leaf nodes of a B+ tree are linked together in the form of a singly linked lists to make the search queries more efficient. 

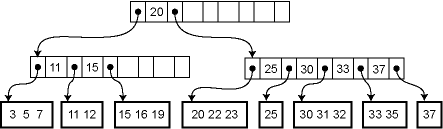
An important concept to be understood before learning B+ tree is multilevel indexing. In multilevel indexing, the index of indices is created as in figure below. It makes accessing the data easier and faster.

 

B+ Tree are used to store the large amount of data which can not be stored in the main memory. Due to the fact that, size of main memory is always limited, the internal nodes (keys to access records) of the B+ tree are stored in the main memory whereas, leaf nodes are stored in the secondary memory.

The internal nodes of B+ tree are often called index nodes. 

WHY B+Tree

• Key are primarily utilized to aid the search by directing to the proper Leaf.
• B+ Tree uses a "fill factor" to manage the increase and decrease in a tree.
• In B+ trees, numerous keys can easily be placed on the page of memory because they do not have the data associated with the interior nodes. Therefore, it will quickly access tree data that is on the leaf node.
• A comprehensive full scan of all the elements is a tree that needs just one linear pass because all the leaf nodes of a B+ tree are linked with each other.

 

Properties of a B+ Tree

1. All leaves are at the same level.
2. The root has at least two children.
3. Each node except root can have a maximum of m children and at least m/2 children.
4. Each node can contain a maximum of m - 1 keys and a minimum of ⌈m/2⌉ - 1 keys.

 

Advantages of B+ Tree

1. Records can be fetched in equal number of disk accesses.
2. Height of the tree remains balanced and less as compare to B tree.
3. We can access the data stored in a B+ tree sequentially as well as directly.
4. Keys are used for indexing.
5. Faster search queries as the data is stored only on the leaf nodes.

 

B+ Tree Applications

• Multilevel Indexing
• Faster operations on the tree (insertion, deletion, search)
• Database indexing

Difference bw B Tree & B+ Tree

In a B tree, search keys and data stored in internal or leaf nodes, whereas In a B+ tree, data stored only in leaf nodes.

The leaves are not connected with each other on a B-tree whereas they are connected on a B+ tree.

Operations on a B+ tree are faster than on a B-tree,  searching of any data in a B+ tree is very easy because all data is found in leaf nodes.