AVL Tree can be defined as height balanced binary search tree in which each node is associated with a balance factor which is calculated by subtracting the height of its right sub-tree from that of its left sub-tree.
AVL tree is a self-balancing binary search tree in which each node maintains extra information called a balance factor whose value is either -1, 0 or +1.
Balance Factor
Balance factor of a node in an AVL tree is the difference between the height of the left subtree and that of the right subtree of that node.
Balance Factor = (Height of Left Subtree - Height of Right Subtree) or (Height of Right Subtree - Height of Left Subtree)
The self balancing property of an avl tree is maintained by the balance factor. The value of balance factor should always be -1, 0 or +1.
An example of a balanced avl tree is:
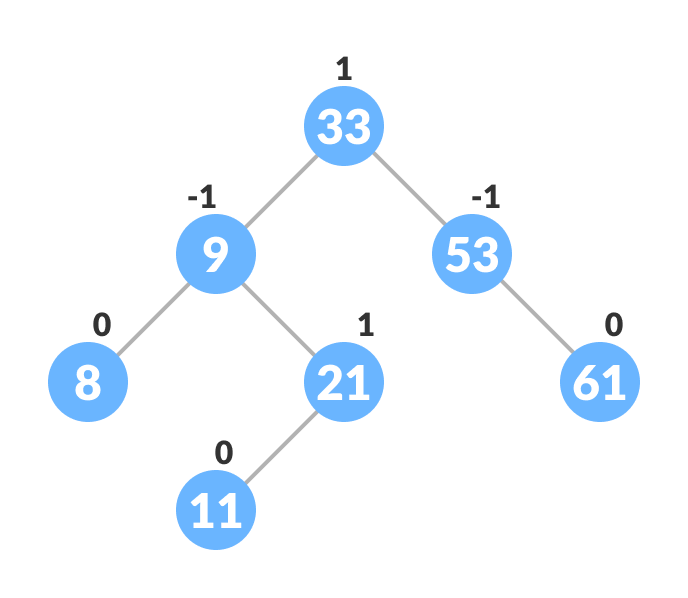
Why?
AVL tree controls the height of the binary search tree by not letting it to be skewed. The time taken for all operations in a binary search tree of height h is O(h). However, it can be extended to O(n) if the BST becomes skewed (i.e. worst case). By limiting this height to log n, AVL tree imposes an upper bound on each operation to be O(log n) where n is the number of nodes.
AVL Rotation
In rotation operation, the positions of the nodes of a subtree are interchanged.
There are two types of rotations: LL, LR, RL, RR
Complexity
O(log n)
AVL Tree Applications
- For indexing large records in databases
- For searching in large databases